2022.07.26 - [👩🏻💻 Develop] - [자료구조] 🚀 이진트리(Binary Tree)
[자료구조] 🚀 이진트리(Binary Tree)
2022.07.25 - [🧐 알고리즘] - [자료구조] 트리(Tree) [자료구조] 트리(Tree) 트리(Tree) 🌲 노드,간선으로 이루어진 비선형 자료 구조 💡 트리의 특징 • 부모노드, 자식노드와 같이 계층구조로 표현되
kong-droid.com
✍️ 우선순위 큐 (Priority Queue)
Queue는 FIFO를 따르지만, 우선순위 큐는 FIFO를 따르지 않고, 우선순위가 높은 데이터를 먼저 출력합니다
Heap을 사용하여 처리합니다 (시간복잡도가 가장 짧습니다)
✍️ 힙 (Heap)
- 완전 이진 트리를 기초로 하며, 최소 혹은 최대값을 빠르게 찾아내도록 만들어진 자료구조입니다
- 부모노드, 자식노드간의 대소관계가 존재합니다
힙의 종류
• 최대힙
부모노드가 자식노드보다 클 때
루트노드가 가장 큰 값

• 최소힙
부모노드가 자식노드보다 작을 때
루트노드가 가장 작은 값

🧐 힙의 구현
힙은 배열로 구현하는 경우가 많습니다
우선, 구현을 하기 전에 각 노드별 인덱스를 보면,
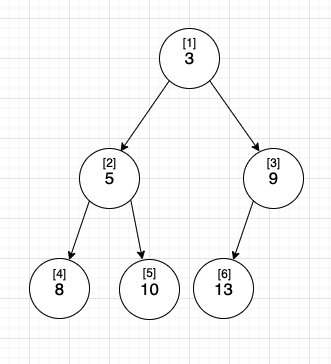
부모노드의 인덱스를 i라고 하면 자식노드의 인덱스는 아래와 같습니다
왼쪽 자식 노드 : 2 * i
오른쪽 자식 노드 : (2 * i)+ 1
부모 노드 : 자식노드 인덱스 / 2
📌 힙의 삽입
(최대힙 기준)
1. 가장 마지막 노드에 값을 삽입
2. 부모노드와 비교
- 부모노드보다 크면 부모노드와 교환, 모든 노드가 최대힙을 만족할 때까지 진행
- 부모노드보다 작으면 동작 종료



fun insertHeap(x: Int) {
maxHeap.add(lastIndex, x)
var i = maxHeap.heapSize
while (i > 1) {
if (maxHeap.get(i / 2) < maxHeap.get(i)) {
swap(i / 2, i)
} else {
break
}
i /= 2
}
}
📌 힙의 삽입
(최대힙 기준)
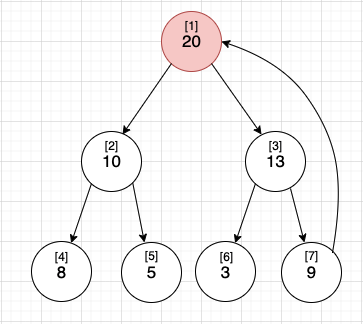
1. 루트 노드 삭제 (루트 노드가 가장 큰 값이므로)
2. 마지막 노드를 루트노드로 가져옴
3. 최대힙 재구성
- 두 개의 자식노드 중 더 큰 값과 교환
- 두 개의 자식노드보다 크면 동작 종료


fun deleteHeap(): Int {
val item: Int = maxHeap.get(1)
maxHeap.get(1) = maxHeap.get(heapSize)
maxHeap.remove(heapSize)
var i = 1
while (i * 2 <= heapSize) {
i = if (maxHeap.get(i) > maxHeap.get(i * 2) && maxHeap.get(i) > maxHeap.get(i * 2 + 1)) {
break
} else if (maxHeap.get(i * 2) > maxHeap.get(i * 2 + 1)) {
swap(i, i * 2)
i * 2
} else {
swap(i, i * 2 + 1)
i * 2 + 1
}
}
return item
}
'🧐 알고리즘' 카테고리의 다른 글
| [자료구조] 🚀 이진트리(Binary Tree) (0) | 2022.07.26 |
|---|---|
| [자료구조] 트리(Tree) (0) | 2022.07.25 |
| [자료구조] 스택 , 큐 , 덱 (0) | 2022.07.17 |