트리(Tree) 🌲
노드, 간선으로 이루어진 비선형 자료 구조
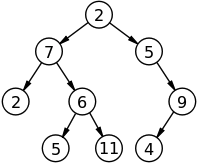
📎 트리의 용어
1. 노드(node): 트리를 구성하는 기본 원소
- 루트 노드 : 트리의 최상위 노드
- 자식 노드 : 어떤 노드 바로 밑에 연결된 노드
- 부모 노드 : 어떤 노드 바로 위에 연결된 노드
- 형제 노드 : 같은 부모 노드를 갖는 노드
- 리프 노드 : 루트 노드를 제외하고 자식이 없는 노드 (가장 마지막 노드들)
2. 높이 : 루트 노드에서부터 가장 깊은 노드까지의 길이 (루트노드에서부터 1로 시작)
3. 깊이(depth): 루트노드에서 어떤 노드까지 거쳐야 하는 간선의 수
4. 레벨 : 트리의 특정 깊이를 가지는 노드의 집합, 루트노드(level = 0)
5. 차수(degree) : 각 노드 별 자식 노드의 개수
6. 트리의 차수 : 트리의 최대 차수
7. 크기(size) : 노드의 개수
📌 트리의 특징
• 부모노드, 자식노드와 같이 계층구조로 표현되는 비선형 자료구조
• 탐색에 주로 사용
• 루트노드를 제외한 모든 노드는 단 하나의 부모노드를 가짐
📌 트리 순회
트리의 모든 노드들을 방문하는 방법을 뜻하는데 크게 3가지로 나뉩니다 🔍
💡 PreOrder (전위순회)
• 루트 ➡️ 왼쪽 자식 노드 ➡️ 오른쪽 자식 노드
[자세한 과정]
- 루트에서 시작
- 왼쪽 트리 순차 순회
- 왼쪽 순회가 끝나면 오른쪽 트리 순차 순회

• DFS(Depth-First-Search)가 전위순회에 해당합니다
💡 InOrder 중위순회(대칭순회)
• 왼쪽 자식 노드 ➡️ 부모 노드 ➡️ 오른쪽 자식 노드
[자세한 과정]
-
- 제일 왼쪽 끝 노드부터 방문, 왼쪽 서브트리를 중위 순회
- 루트를 거칩니다
- 오른쪽에 남은 트리를 순회합니다

🚩 출력 순서
4 -> 3 -> 2 -> 1 -> 7 -> 6 -> 5 -> 8 -> 9 -> 10
💡 PostOrder (후위순회)
• 왼쪽 자식 노드 ➡️ 오른쪽 자식 노드 ➡️ 부모노드
[자세한 과정]
-
- 제일 왼쪽 끝 노드부터 방문, 왼쪽 서브트리를 중위 순회
- 루트를 거치지 않고 오른쪽의 트리들을 순회
- 루트를 마지막으로 방문
• 자식 노드 모두 방문 후 부모 노드를 방문
• 노드 삭제 시 사용

🚩 출력 순서
4 -> 3 -> 2 -> 7 -> 6 -> 8 -> 5 -> 10 -> 9 -> 1
중요한 자료 구조 중 하나인 트리에 대해 알아봤습니다
궁금하신 점이나 의견이 있으시면 댓글 부탁드립니다 감사합니다 😊
'🧐 알고리즘' 카테고리의 다른 글
| [자료구조] 🚀 우선순위 큐 & 힙(Heap) (0) | 2022.07.27 |
|---|---|
| [자료구조] 🚀 이진트리(Binary Tree) (0) | 2022.07.26 |
| [자료구조] 스택 , 큐 , 덱 (0) | 2022.07.17 |